Home

# 归并排序（稳定）

归并排序是建立在归并操作上的一种有效的排序算法，1945 年由约翰・冯・诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。

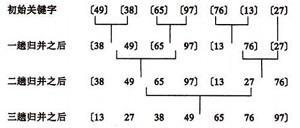
# 1、基本思想

归并排序算法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

# 2、算法描述

归并排序可通过两种方式实现：

  • 自上而下的递归
  • 自下而上的迭代
    一、递归法（假设序列共有 n 个元素）：

①. 将序列每相邻两个数字进行归并操作，形成 floor(n/2) 个序列，排序后每个序列包含两个元素；
②. 将上述序列再次归并，形成 floor(n/4) 个序列，每个序列包含四个元素；
③. 重复步骤②，直到所有元素排序完毕。

二、迭代法

①. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
②. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
③. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
④. 重复步骤③直到某一指针到达序列尾
⑤. 将另一序列剩下的所有元素直接复制到合并序列尾

# 3、代码实现

归并排序其实要做两件事：

  • 分解：将序列每次折半拆分
  • 合并：将划分后的序列段两两排序合并
    因此，归并排序实际上就是两个操作，拆分 + 合并

如何合并？

L[first…mid] 为第一段， L[mid+1…last] 为第二段，并且两端已经有序，现在我们要将两端合成达到 L[first…last] 并且也有序。

首先依次从第一段与第二段中取出元素比较，将较小的元素赋值给 temp[]
重复执行上一步，当某一段赋值结束，则将另一段剩下的元素赋值给 temp[]
此时将 temp[] 中的元素复制给 L[] ，则得到的 L[first…last] 有序

如何分解？

在这里，我们采用递归的方法，首先将待排序列分成 A,B 两组；然后重复对 A、B 序列
分组；直到分组后组内只有一个元素，此时我们认为组内所有元素有序，则分组结束。

这里我写了递归算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * 归并排序（递归）
 *
 * ①. 将序列每相邻两个数字进行归并操作，形成 floor(n/2)个序列，排序后每个序列包含两个元素；
 * ②. 将上述序列再次归并，形成 floor(n/4)个序列，每个序列包含四个元素；
 * ③. 重复步骤②，直到所有元素排序完毕。
 * @param arr	 待排序数组
 */
public static int[] mergingSort(int[] arr){
    if(arr.length <= 1) return arr;

    int num = arr.length >> 1;
    int[] leftArr = Arrays.copyOfRange(arr, 0, num);
    int[] rightArr = Arrays.copyOfRange(arr, num, arr.length);
    System.out.println("split two array: " + Arrays.toString(leftArr) + " And " + Arrays.toString(rightArr));
    return mergeTwoArray(mergingSort(leftArr), mergingSort(rightArr));      //不断拆分为最小单元，再排序合并
}

private static int[] mergeTwoArray(int[] arr1, int[] arr2){
    int i = 0, j = 0, k = 0;
    int[] result = new int[arr1.length + arr2.length];  //申请额外的空间存储合并之后的数组
    while(i < arr1.length && j < arr2.length){      //选取两个序列中的较小值放入新数组
        if(arr1[i] <= arr2[j]){
            result[k++] = arr1[i++];
        }else{
            result[k++] = arr2[j++];
        }
    }
    while(i < arr1.length){     //序列1中多余的元素移入新数组
        result[k++] = arr1[i++];
    }
    while(j < arr2.length){     //序列2中多余的元素移入新数组
        result[k++] = arr2[j++];
    }
    System.out.println("Merging: " + Arrays.toString(result));
    return result;
}

由上，长度为 n 的数组，最终会调用 mergeSort 函数 2n-1 次。通过自上而下的递归实现的归并排序，将存在堆栈溢出的风险。

链接

Edited on Views times