# 布隆过滤器

# 什么是布隆过滤器

布隆过滤器（ Bloom Filter ），是 1970 年，由一个叫布隆的小伙子提出的，距今已经五十年了，和老哥一样老。

它实际上是一个很长的二进制向量和一系列随机映射函数，二进制大家应该都清楚，存储的数据不是 0 就是 1 ，默认是 0 。

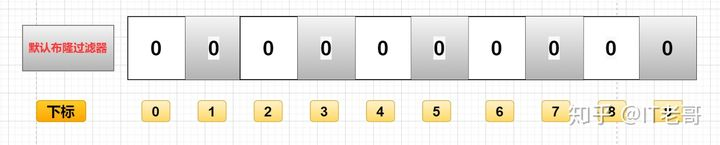
主要用于判断一个元素是否在一个集合中， 0 代表不存在某个数据， 1 代表存在某个数据。

懂了吗？作为暖男的老哥在给你们画张图来帮助理解：

# 布隆过滤器用途

解决 Redis 缓存穿透（今天重点讲解）
在爬虫时，对爬虫网址进行过滤，已经存在布隆中的网址，不在爬取。
垃圾邮件过滤，对每一个发送邮件的地址进行判断是否在布隆的黑名单中，如果在就判断为垃圾邮件。

以上只是简单的用途举例，大家可以举一反三，灵活运用在工作中。

# 布隆过滤器原理

存入过程

布隆过滤器上面说了，就是一个二进制数据的集合。当一个数据加入这个集合时，经历如下洗礼（这里有缺点，下面会讲）：

通过 K 个哈希函数计算该数据，返回 K 个计算出的 hash 值
这些 K 个 hash 值映射到对应的 K 个二进制的数组下标
将 K 个下标对应的二进制数据改成 1。
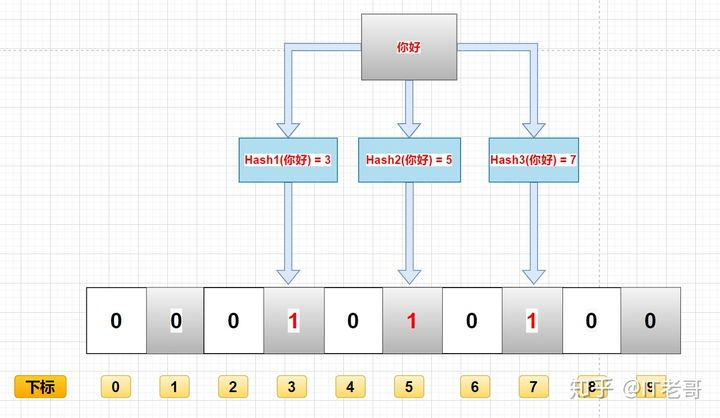
例如，第一个哈希函数返回 x，第二个第三个哈希函数返回 y 与 z，那么： X、Y、Z 对应的二进制改成 1。

如图所示：

查询过程
布隆过滤器主要作用就是查询一个数据，在不在这个二进制的集合中，查询过程如下：

通过 K 个哈希函数计算该数据，对应计算出的 K 个 hash 值
通过 hash 值找到对应的二进制的数组下标
判断：如果存在一处位置的二进制数据是 0 ，那么该数据不存在。如果都是 1 ，该数据存在集合中。（这里有缺点，下面会讲）

删除过程
一般不能删除布隆过滤器里的数据，这是一个缺点之一，我们下面会分析。

# 布隆过滤器的优缺点

优点
由于存储的是二进制数据，所以占用的空间很小
它的插入和查询速度是非常快的，时间复杂度是 O（K） ，可以联想一下 HashMap 的过程
保密性很好，因为本身不存储任何原始数据，只有二进制数据
缺点
这就要回到我们上面所说的那些缺点了。

添加数据是通过计算数据的 hash 值，那么很有可能存在这种情况：两个不同的数据计算得到相同的 hash 值。

例如图中的 “你好” 和 “hello”，假如最终算出 hash 值相同，那么他们会将同一个下标的二进制数据改为 1。

这个时候，你就不知道下标为 2 的二进制，到底是代表 “你好” 还是 “hello”。

# 由此得出如下缺点：

存在误判
假如上面的图没有存 "hello" ，只存了" 你好 "，那么用 "hello" 来查询的时候，会判断 "hello" 存在集合中。

因为 “你好” 和 “hello” 的 hash 值是相同的，通过相同的 hash 值，找到的二进制数据也是一样的，都是 1。

删除困难

到这里我不说大家应该也明白为什么吧，作为你们的暖男老哥，还是讲一下吧。

还是用上面的举例，因为 “你好” 和 “hello” 的 hash 值相同，对应的数组下标也是一样的。

这时候老哥想去删除 “你好”，将下标为 2 里的二进制数据，由 1 改成了 0 。

那么我们是不是连 “hello” 都一起删了呀。（ 0 代表有这个数据， 1 代表没有这个数据）

# 实现布隆过滤器

引入依赖

<dependency>
  <groupId>com.google.guava</groupId>
  <artifactId>guava</artifactId>
  <version>29.0-jre</version>
</dependency>

public class BloomFilterCase {

    /**
     * 预计要插入多少数据
     */
    private static int size = 1000000;

    /**
     * 期望的误判率
     */
    private static double fpp = 0.01;

    /**
     * 布隆过滤器
     */
    private static BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(),size,fpp);


    public static void main(String[] args) {
        //插入10万条样本数据
        for (int i = 0; i < size; i++) {
            bloomFilter.put(i);
        }

        //用另外十万条测试数据,测试误判率
        int count = 0;
        for (int i = size; i < size + 1000000; i++) {
            if (bloomFilter.mightContain(i)){
                count++;
                System.out.println(i+"误判了");
            }
        }

        System.out.println("总共误判了:" + count);
    }


}

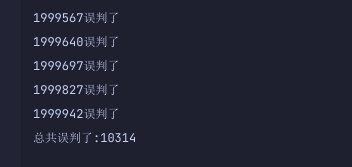
100 万数据里有 947 个误判，约等于 0.01% ，也就是我们代码里设置的误判率： fpp = 0.01。

# 深入分析代码

核心 BloomFilter.create 方法

@VisibleForTesting
  static <T> BloomFilter<T> create(
      Funnel<? super T> funnel, long expectedInsertions, double fpp, Strategy strategy) {
    。。。。
}

这里有四个参数：

funnel ：数据类型 (一般是调用 Funnels 工具类中的)
expectedInsertions ：期望插入的值的个数
fpp ：误判率 (默认值为 0.03 )
strategy ：哈希算法

我们重点讲一下 fpp 参数

# 情景总结

误判率可以通过 fpp 参数进行调节
fpp 越小，需要的内存空间就越大： 0.0 1 需要 900 多万位数， 0.03 需要 700 多万位数。
fpp 越小，集合添加数据时，就需要更多的 hash 函数运算更多的 hash 值，去存储到对应的数组下标里。（忘了去看上面的布隆过滤存入数据的过程）

上面的 numBits ，表示存一百万个 int 类型数字，需要的位数为 7298440 ， 700 多万位。理论上存一百万个数，一个 int 是 4 字节 32 位，需要 481000000=3200 万位。如果使用 HashMap 去存，按 HashMap50% 的存储效率，需要 6400 万位。可以看出 BloomFilter 的存储空间很小，只有 HashMap 的 1/10 左右

上面的 numHashFunctions 表示需要几个 hash 函数运算，去映射不同的下标存这些数字是否存在（ 0 or 1 ）。

# 解决 `Redis` 缓存雪崩

上面使用 Guava 实现的布隆过滤器是把数据放在了本地内存中。分布式的场景中就不合适了，无法共享内存。

我们还可以用 Redis 来实现布隆过滤器，这里使用 Redis 封装好的客户端工具 Redisson 。

其底层是使用数据结构 bitMap ，大家就把它理解成上面说的二进制结构，由于篇幅原因， bitmap 不在这篇文章里讲

代码实现

pom 配置：

<dependency>
  <groupId>org.redisson</groupId>
  <artifactId>redisson-spring-boot-starter</artifactId>
  <version>3.13.4</version>
</dependency>

Java 代码

public class RedissonBloomFilter {

  public static void main(String[] args) {
    Config config = new Config();
    config.useSingleServer().setAddress("redis://127.0.0.1:6379");
    config.useSingleServer().setPassword("1234");
    //构造Redisson
    RedissonClient redisson = Redisson.create(config);

    RBloomFilter<String> bloomFilter = redisson.getBloomFilter("phoneList");
    //初始化布隆过滤器：预计元素为100000000L,误差率为3%
    bloomFilter.tryInit(100000000L,0.03);
    //将号码10086插入到布隆过滤器中
    bloomFilter.add("10086");

    //判断下面号码是否在布隆过滤器中
    //输出false
    System.out.println(bloomFilter.contains("123456"));
    //输出true
    System.out.println(bloomFilter.contains("10086"));
  }
}